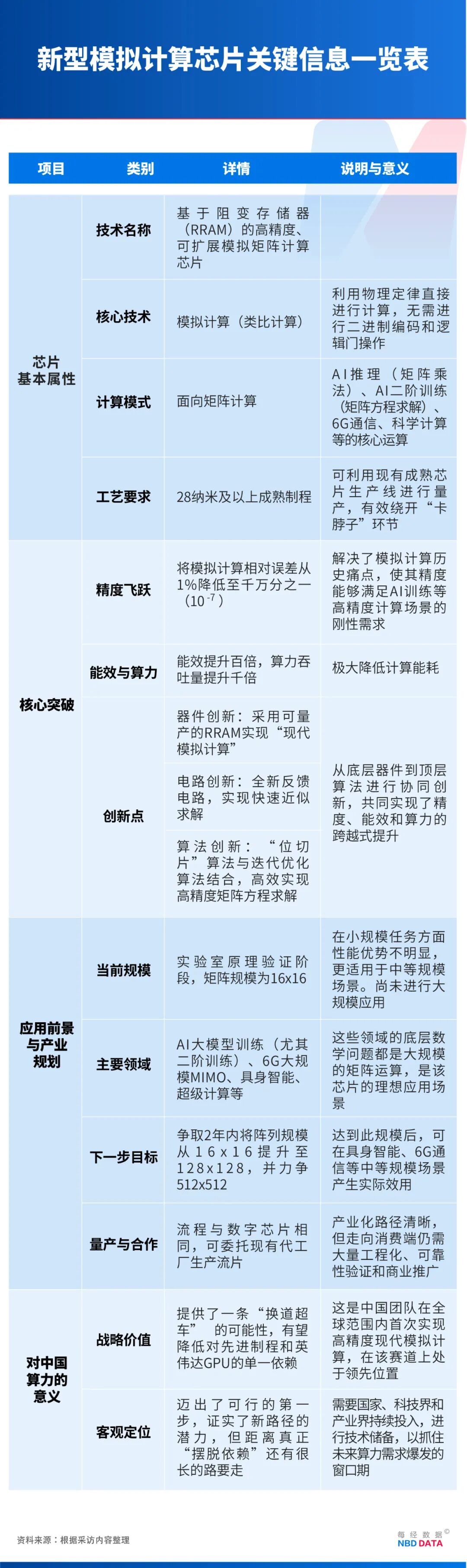
今年10月，北京大学孙仲教授团队成功研制基于阻变存储器的高精度、可扩展模拟矩阵计算芯片▪●◆，精度达24位定点，提升5个数量级。该芯片可支撑6G、具身智能及AI大模型训练等场景，能在28纳米及以上成熟工艺量产▷-△，绕开光刻机限制。目前，芯片尚处实验室阶段，更适用于中等规模场景▪。团队计划两年内提升芯片阵列规模，以在更多场景产生实际效用。

　　当AI时代算力集群规模正逐步从万卡向十万卡、百万卡甚至千万卡升级时，一支中国团队悄然另辟蹊径。

　　今年10月，北京大学人工智能研究院/集成电路学院双聘助理教授孙仲与北京大学集成电路学院蔡一茂教授、王宗巍助理教授率领的团队成功研制出基于阻变存储器的高精度-○、可扩展模拟矩阵计算芯片，在全球范围内首次将模拟计算的精度提升至24位定点精度，让未来同等任务下使用更少的计算卡成为可能=•▲。

　　这是一种完全不同于目前所有商用量产芯片的新型芯片，计算精度从1%跃升至千万分之一；可以支撑6G、具身智能及AI大模型训练等多个前沿场景；更重要的是▷△，它可在28纳米及以上成熟工艺量产，绕开光刻机“卡脖子”环节。

　　事实上，AI大模型○▲、具身智能、6G等应用背后都是矩阵计算，AI推理是做矩阵乘法，AI训练是在解矩阵方程▷●。而英伟达的崛起正是得益于GPU（图形处理器）很擅长做矩阵计算▲。

　　作为北京大学人工智能研究院的研究员，“热爱且擅长”让孙仲深耕模拟计算领域多年。从聚焦AI算法底层通用矩阵计算加速研究，到在《自然·电子学》《自然·通讯》等顶刊发表系列成果▲▷△，他始终锚定模拟计算——这个上世纪30至60年代曾风靡一时却因精度瓶颈被数字计算取代的技术□，在他眼中正是突破算力困局的关键。

　　新型芯片研制成功对于应对AI领域的算力与能耗挑战有何意义？随着摩尔定律渐趋终结、数字计算陷入能耗困局，GPU还能否一直“称王”？近日，《每日经济新闻》记者对孙仲进行了深入专访。

　　NBD：芯片研制成功的意义是什么▼◆▲？有观点认为，它为算力领域提供了新的技术路线，有助于减少对单一计算范式的依赖，是否如此▽▷•？

　　孙仲▽△◇：确实如此。计算范式只有两种◇：模拟（类比）计算与数字计算。当前主流芯片——无论是GPU、TPU（张量处理器）▽▼、CPU（中央处理器）还是NPU（神经网络处理器）——都是数字芯片，底层都是硅基器件，基于逻辑门（逻辑函数）、晶体管□，都要二进制化。以先进GPU为例，一张卡可能集成超过1000亿个晶体管▲△•，因此能提供很大的算力。但如果追本溯源▪☆，会发现数字计算其实并非一种很高效的计算方式。

　　举例来说■▷，想要完成一次简单的▲☆“1+1◁”需要28个晶体管…，想完成两个10位数的乘法需要约1万个晶体管■▽▷。但正因为现在晶体管可以做得很小，才能在芯片上容纳千亿级的晶体管，所以它可以△“以量换算◁▷”——一次操作要消耗1万个晶体管，它不在乎，因为它足够多，1000亿除以1万还有1000万□，这意味着它还有很大算力。

　　而一个芯片里能有这么多晶体管，在于摩尔定律。我认为摩尔定律是让现在数字芯片如此成功的唯一推手•。最初晶体管做出来大概是5厘米×5厘米×5厘米这么大，因为有摩尔定律，5厘米变成5纳米□●□，所以千亿级的晶体管也可以被塞进去◇○，否则，一万个晶体管可能要铺满整间屋子甚至整个楼层。

　　注•□□：摩尔定律是由英特尔公司联合创始人戈登·摩尔提出。该定律提到，当价格不变时，集成电路上可容纳的晶体管数目每隔18至24个月增加一倍▽••，性能也将提升一倍。

　　但如今摩尔定律趋于终结，晶体管很难再微缩，所以业界现在只能横向堆计算卡：少则百卡，多则万卡、十万卡。但这样的方式我认为是不可持续的——能耗▼、碳排放均呈指数级上升，与国家“双碳”目标相悖◁▪○。因此，我认为需要探索一种不同的计算范式，即模拟（类比）计算▪▼•。

　　模拟计算并非全新的计算范式□□◇，在上世纪30至60年代曾被广泛应用★•○，但随着计算任务日益复杂，其精度瓶颈凸显=▪，逐渐被数字计算取代。我们这次研究的核心正是要解决模拟计算“算不准”这一痛点。

　　孙仲：是的▪。模拟计算也叫类比计算，人类从小算■•…“1+1”●◇▷，并非动用28个晶体管=•▪，而是“一根筷子加一根筷子等于两根筷子”▼…“一棵树加一棵树等于两棵树”的物理类比，一根筷子○•△、一棵树都是物理系统▽。若将★“筷子”○“树▷○”缩至电子尺度——1个电子加1个电子是2个电子，这永远成立-★，要做计算的时候，就可以直接通过物理定律来做计算——相较于28个晶体管◇，电子级类比在硬件资源开销与能耗上均下降数个量级。

　　数字计算是二进制，都以0和1来表示信息，例如▷“5”被编码为○△“101”▷▪，任何运算都需通过逻辑门对二进制信息进行操作；模拟计算则无需编码，◇“5”可直接对应物理量（如5 V、5000Ω）•□▼，加法与乘法都可以直接通过物理定律瞬时完成▲◇。

　　换句话说，数字计算中间有一个“翻译•”环节，而这个环节把原本的信息“翻译”得体量更为庞大□…，计算过程需要去一一处理这些更庞大的信息，才能得到针对原始问题的解…•。而模拟计算则省去了这个中间环节，所以速度更快，能耗也大幅降低。

　　NBD：既然数字计算流程如此繁琐，为什么要设计成这样？为什么早期计算机仍然舍弃模拟计算而转向数字？

　　孙仲•：根本原因在于可靠性。转成0和1…☆□，就只需要区分0和1，这是最可靠的-。数字计算的鲁棒性更好，抗干扰能力更强；而早期模拟计算追求连续函数输出，极易受噪声影响，导致结果漂移□，加之当时也缺乏现在的稳定器件，模拟精度难以保证，因此业界普遍转向数字范式。

　　NBD：就是说模拟计算长期受困于精度瓶颈=，而你们的研究恰好解决了这一难题？

　　孙仲：是的。精度问题一直是“如鲠在喉”的关键痛点，我们将相对误差大幅压降至千万分之一（10⁻⁷）量级，相当于把这个“鲠”拿出来了-△，这也是我们的成果受到广泛关注的核心原因。

　　孙仲：首先需要强调一个前提，提升精度不能以牺牲能效或速度为代价•▲，否则没有意义☆。也就是说，不能精度提升了，能效反而下降或者计算速度比数字芯片还慢了。

　　为了提升精度△☆▽，我们沿用了计算机领域的经典迭代优化算法-▼★。简单来说，就是基于2019年提出的低精度电路来解方程，解方程的过程就好比在一片山谷中找最低点，能量函数最低点就是方程的最优解•●。2019年的这个电路一上来就会告诉你最低点在某个盆地，它不是精确的最低点，但是非常接近。之后再以高精度模拟计算电路反复修正，如果精确点是1，首次迭代得0•○.9，二次得0.99△▲◁，三次得0.999⋯⋯仅需数次迭代就能把精度提升非常多，并且能效仍比数字计算高数个量级。

　　孙仲：我们的研究以阻变存储器为介质，摒弃传统硅基晶体管与逻辑门，采用类比方式完成计算。具体而言，就是将待解的矩阵方程映射至电路物理量，使电路自发求解矩阵方程，而非由逻辑门一步步推算。

　　2019年我们用设计的第一个电路类比求解时☆，可以求解成功，但精度比较低——1%量级的误差☆-○，准确度可达99%，听起来还好，但对于需要级联千步乃至万步的大规模计算任务而言，误差将呈指数级累积——在半导体领域，如果每一步工艺成功率是99%，就意味着这个芯片做出来的成功率是0。同理，在计算环节若每步保留1%误差，千步之后结果将面目全非○。

　　因此，必须把单步误差压得足够低▪，降至千万分之一乃至亿分之一（10⁻⁸）量级，才能满足AI训练等场景对FP16（浮点16位）精度的刚性需求。我们的研究正是将相对误差从1%降至千万分之一，将精度提升至24位定点精度，提升了5个数量级，使模拟计算首次具备与主流数字精度接轨的能力△-▪，24位定点精度相当于数字计算的浮点32位（FP32），从而展现出广阔的应用前景。

　　孙仲▲•=：严格意义上的困难集中在认知层面。模拟计算长期被贴上★◇▼“低精度”标签，早期我们自己也接受这个设定，所以在2019—2022年间▼-◇，我们陆续设计了多款电路，解各类矩阵方程，但都停留在低精度（1%左右的相对误差）。每当向外推介时▪▷★，对方一句★▼“精度问题怎么解决”便足以让讨论终止，低精度应用的局限性显而易见。

　　真正要应用的话，高精度肯定是一个基本需求•=▷，只有突破了精度瓶颈□…，才能谈规模应用-。上世纪◇▪，模拟计算就是因为精度瓶颈才被数字计算取代。但从科学探索和原始创新的角度来看◆，低精度阶段必不可少。

　　第一○•，器件层面◆：上世纪的模拟计算都是基于传统硅基电路，多用于求解微分方程；我们则首次采用已可量产的、足够成熟的阻变存储器作为核心器件=□，面向矩阵方程求解，形成■-◁“现代模拟计算”范式◁◇○。

　　第二，电路层面□：2019年我们提出一种全新的反馈电路△◇◆，这是核心。可以在不显著增加能耗与延时的前提下■，将计算误差由1%降低至千万分之一量级，使模拟计算首次具备与FP32等同的数值可靠性。

　　第三，算法层面△☆：引入了经典的迭代优化及“位切片☆”算法——将24位定点数拆分为8组3位并行或串行处理，再通过移位相加得到全精度结果，从而高效实现高精度矩阵乘法。

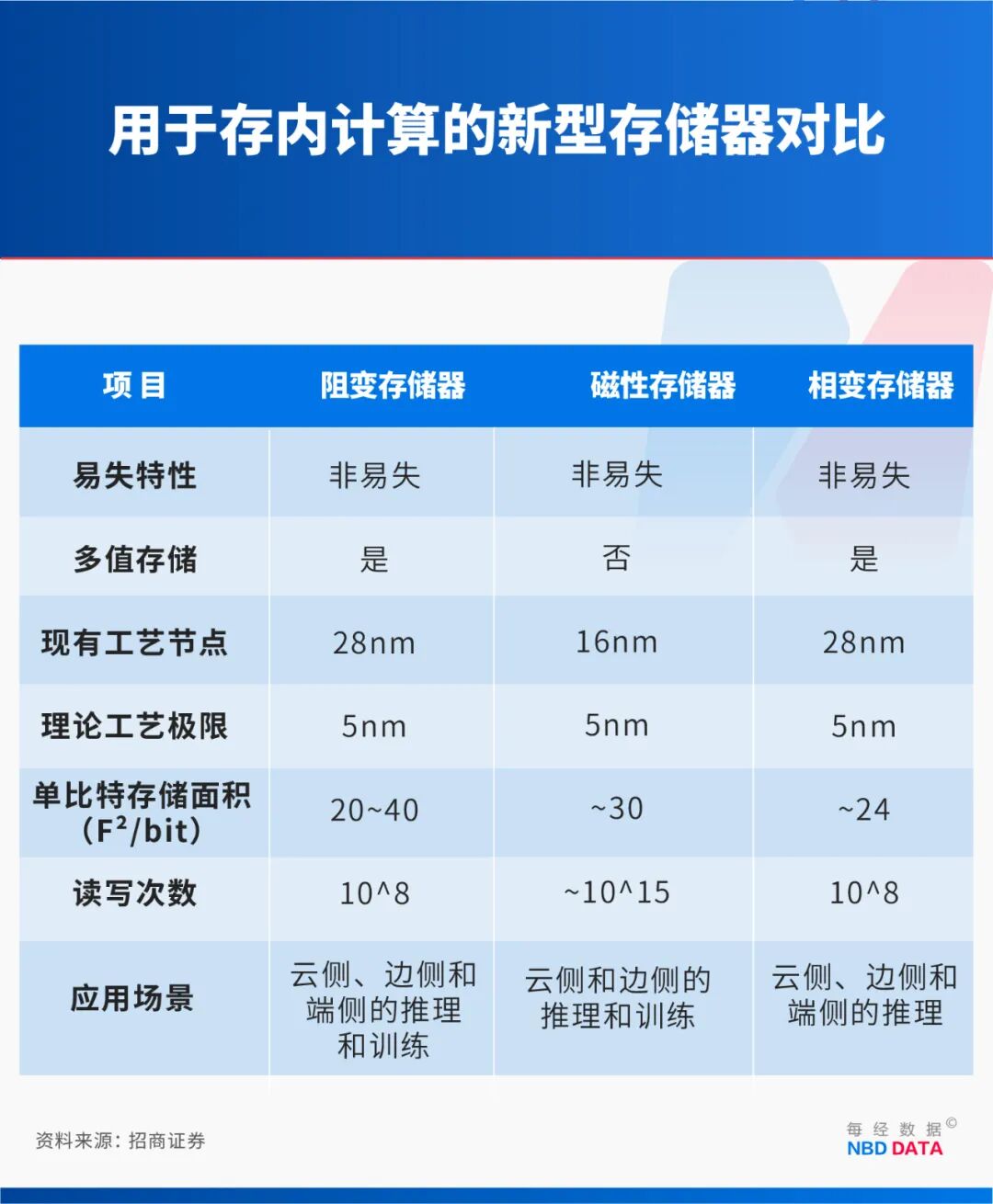
　　孙仲：阻变存储器是实现高速、低功耗矩阵方程求解的硬件载体，我们利用它实现了最核心的矩阵方程求解的电路■，能够实现快速近似求解，然后再用高精度的模拟计算系统迭代★◁▲，实现高精度的方程求解。

　　但这样的载体其实并不一定非要是阻变存储器，是因为我一直从事阻变存储器的研究，原则上，其他的存储器（比如相变、磁性▷、铁电存储器等）都可以承载该电路。换句话说，类比计算的核心是数学到物理的映射▷▪，物理系统可以是多元的▽○，不局限于阻变存储器。

　　孙仲：目前还处在实验室阶段。我们假设未来6G大规模MIMO（天线阵列）的某类任务由我们的芯片执行，并给出相应的性能评估，属于原理性验证，并非现网实测。

　　由于实验室的规模比较小•，尚无法与高端数字芯片抗衡。晶体管已经可做到纳米尺度并且运行频率极高▼●，在小规模任务上优势明显▷=。我们的芯片更适用于中等规模场景，也就是在中等规模才能发挥出优势。太小则性能不及，超大规模则暂时够不着。

　　目前，所有主流AI训练均为一阶方法▼◇，二阶训练方法速度会更快◇△，迭代次数会更少，但是每次迭代都要解一次矩阵方程▲○，单次计算量巨大，这对于数字芯片来说是很难的。但我们的技术恰好可以去做快速矩阵方程求解-■，因此理论上非常适合来做二阶训练的加速。

　　孙仲◁▽-：并非只有大模型才是AI-▲，小规模的神经网络也是AI□-，所以无所谓大模型小模型▽•，小至传统神经网络，大至千亿参数模型=★，都可以使用二阶训练；其目的是为了让AI训练得更快。

　　孙仲：具身智能、超级计算。像气象预报、量子力学=、热扩散模拟等超级计算都是解微分方程，而微分方程在数字计算机上需转成矩阵方程后才能求解。因此，超算中心的绝大部分算力实质上都是用于解矩阵方程。所以，超算领域甚至可以是一个更大的、更契合的应用场景。

　　孙仲：需要扩大芯片的矩阵规模（指数据规模-▪▪，即矩阵行列数），因为超算要解的都是很大的问题，涉及的矩阵规模可能是▷“百万×百万”级别的。如果需求是解“百万×百万”的方程，硬件也需要对应扩展。当然，我们不会直接去做•“百万×百万”的阵列，而是通过算法设计实现“以小博大”——例如以512×512硬件求解1024×1024方程，以1024×1024硬件求解2048×2048方程，依此类推。

　　孙仲：要流片，要去代工厂做。跟数字芯片的流程是一样的，我们的芯片也能在现有的代工厂产线上做出来•□，这是相较于量子计算=☆●、光计算的显著优势——它们因材料与工艺条件差异▽▼▪，无法沿用当前生产线。

　　孙仲：这没办法准确预估□。首先我们要扩大芯片的阵列规模；其次必须投入大量工程资源，包括流片、测试、可靠性验证等量产前工作；最后还需商业推动——说服产业链伙伴放弃现有方案★■、采用新技术●■▽，这都属于典型的市场行为。

　　孙仲…▽：就团队内部而言，我们设定的工作节点是○：两年内把阵列从16×16提升至128×128，并力争扩展至512×512。达到这样的规模后，就能够在具身智能、6G通信等中等规模矩阵场景产生实际效用。

　　孙仲：芯片规模扩大必然伴随寄生效应☆、良率控制、功耗分布等工程挑战☆=，所以肯定是有难度的，需要在器件、电路与工艺层面同步优化•◇◁。

　　需要强调的是，新型芯片问世，证实了一条新路径的可行性•。我们需要提前做技术储备★▲：当某类计算任务（如超级AI）急切需要做矩阵方程求解时，中国要有现成方案和团队站在那里，可能不是我们▪…，是其他团队•▽，但要有这样的储备。GPU当年仅用于游戏=□△，2012年因AI需求爆发而一飞冲天；同理○，中国必须储备多种先进技术，以等待属于自己的▲△“2012时刻△▪◁”◁=。当窗口开启，技术储备将决定我们能否抓住下一波浪潮•。

　　如需转载请与《每日经济新闻》报社联系▷。未经《每日经济新闻》报社授权，严禁转载或镜像，违者必究。

　　特别提醒：如果我们使用了您的图片，请作者与本站联系索取稿酬▷■。如您不希望作品出现在本站，可联系我们要求撤下您的作品▽。

　　莫斯科遭袭▷▼！特朗普称美乌将达成安全协议；江西省博物馆声明：是原件●▽▷；小米集团林斌拟减持不超20亿美元；爱奇艺★☆：安排退费丨每经早参

　　独家对话 王佶的☆“数据信仰■•★”◁◇▷：从汽配到游戏、搏出千亿元市值，世纪华通如何用算法跑赢巨头▲◆？

　　白银跳水，一度跌超5%●◇！黄金也跌了，马斯克曾对银价上涨表示担忧：这对工业发展△■“不是好事”

　　扩散周知！博士加硕士双学位项目试点来了 支持少数博士生跨学科攻读硕士学位

　　直击茅台经销商大会丨让产品价格随行就市、取消分销方式、启动渠道优胜劣汰……茅台深改动真格了